what transformation change the graph of f(x) to the graph of g(x)

Learning Objectives

In this section, you will:

• Graph functions using vertical and horizontal shifts.
• Graph functions using reflections about the[latex]\,x\text{-centrality}\,[/latex] and the[latex]\,y\text{-axis}.[/latex]
• Determine whether a function is even, odd, or neither from its graph.
• Graph functions using compressions and stretches.
• Combine transformations.

Figure 1. (credit: "Misko"/Flickr)

We all know that a flat mirror enables the states to come across an accurate image of ourselves and whatsoever is behind us. When we tilt the mirror, the images nosotros see may shift horizontally or vertically. But what happens when we bend a flexible mirror? Like a carnival funhouse mirror, it presents united states with a distorted image of ourselves, stretched or compressed horizontally or vertically. In a like fashion, we can distort or transform mathematical functions to meliorate adapt them to describing objects or processes in the real world. In this section, we will take a look at several kinds of transformations.

Graphing Functions Using Vertical and Horizontal Shifts

Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. One method we tin can employ is to accommodate the basic graphs of the toolkit functions to build new models for a given scenario. At that place are systematic ways to alter functions to construct appropriate models for the problems nosotros are trying to solve.

Identifying Vertical Shifts

One elementary kind of transformation involves shifting the unabridged graph of a function upward, down, right, or left. The simplest shift is a vertical shift, moving the graph upwardly or downwards, considering this transformation involves adding a positive or negative constant to the part. In other words, nosotros add the same constant to the output value of the office regardless of the input. For a part[latex]\,thou\left(x\right)=f\left(x\correct)+g,\,[/latex]the function[latex]\,f\left(x\right)\,[/latex]is shifted vertically[latex]\,k\,[/latex]units. See (Figure) for an example.

Figure 2. Vertical shift by[latex]\,one thousand=ane\,[/latex]of the cube root part[latex]\,f\left(x\right)=\sqrt[3]{10}.[/latex]

To assist you visualize the concept of a vertical shift, consider that[latex]\,y=f\left(ten\right).\,[/latex]Therefore,[latex]\,f\left(ten\right)+k\,[/latex]is equivalent to[latex]\,y+k.\,[/latex]Every unit of measurement of[latex]\,y\,[/latex]is replaced by[latex]\,y+k,\,[/latex]so the y-value increases or decreases depending on the value of[latex]\,yard.\,[/latex]The result is a shift upward or downward.

Vertical Shift

Given a function [latex]f\left(x\correct),[/latex] a new function [latex]g\left(x\correct)=f\left(ten\right)+thousand,[/latex] where [latex]\,m[/latex] is a constant, is a vertical shift of the office [latex]f\left(x\right).[/latex] All the output values change by [latex]m[/latex] units. If [latex]k[/latex] is positive, the graph will shift up. If [latex]k[/latex] is negative, the graph will shift down.

Adding a Abiding to a Function

To regulate temperature in a greenish building, airflow vents near the roof open and close throughout the 24-hour interval. (Effigy) shows the expanse of open up vents[latex]\,Five\,[/latex](in foursquare feet) throughout the day in hours later on midnight,[latex]\,t.\,[/latex]During the summer, the facilities manager decides to endeavor to better regulate temperature by increasing the corporeality of open vents by xx square feet throughout the day and dark. Sketch a graph of this new function.

Figure 3.

How To

Given a tabular function, create a new row to correspond a vertical shift.

1. Identify the output row or column.
2. Determine the magnitude of the shift.
3. Add the shift to the value in each output cell. Add together a positive value for up or a negative value for downwardly.

Shifting a Tabular Function Vertically

A function[latex]\,f\left(x\right)\,[/latex]is given in (Figure). Create a table for the part[latex]\,g\left(x\right)=f\left(x\correct)-three.[/latex]

[latex]x[/latex]	2	4	6	8
[latex]f\left(x\right)[/latex]	1	3	seven	11

Analysis

As with the earlier vertical shift, notice the input values stay the same and just the output values modify.

Try It

The function[latex]\,h\left(t\right)=-four.9{t}^{2}+30t\,[/latex]gives the height[latex]\,h\,[/latex]of a ball (in meters) thrown upward from the ground afterward[latex]\,t\,[/latex]seconds. Suppose the ball was instead thrown from the top of a 10-m edifice. Relate this new height function[latex]\,b\left(t\right)\,[/latex]to[latex]\,h\left(t\right),\,[/latex]and then find a formula for[latex]\,b\left(t\right).[/latex]

Identifying Horizontal Shifts

We just saw that the vertical shift is a alter to the output, or exterior, of the office. We will now look at how changes to input, on the within of the role, change its graph and meaning. A shift to the input results in a movement of the graph of the role left or right in what is known as a horizontal shift, shown in (Figure).

Effigy 5. Horizontal shift of the office[latex]\,f\left(10\correct)=\sqrt[three]{ten}.\,[/latex]Note that[latex]\,h=+ane\,[/latex]shifts the graph to the left, that is, towards negative values of[latex]\,x.[/latex]

For example, if[latex]\,f\left(x\right)={10}^{2},\,[/latex]and so[latex]\,one thousand\left(10\right)={\left(x-2\correct)}^{2}\,[/latex]is a new function. Each input is reduced by 2 prior to squaring the function. The issue is that the graph is shifted 2 units to the right, because nosotros would need to increase the prior input by 2 units to yield the same output value equally given in[latex]\,f.[/latex]

Horizontal Shift

Given a function[latex]\,f,\,[/latex]a new role[latex]\,g\left(x\right)=f\left(ten-h\right),\,[/latex]where[latex]\,h\,[/latex]is a constant, is a horizontal shift of the role[latex]\,f.\,[/latex]If[latex]\,h\,[/latex]is positive, the graph will shift right. If[latex]\,h\,[/latex]is negative, the graph will shift left.

Adding a Constant to an Input

Returning to our building airflow case from (Figure), suppose that in autumn the facilities manager decides that the original venting plan starts likewise late, and wants to begin the entire venting plan ii hours earlier. Sketch a graph of the new part.

Analysis

Note that[latex]\,V\left(t+2\right)\,[/latex]has the issue of shifting the graph to the left.

Horizontal changes or "inside changes" affect the domain of a office (the input) instead of the range and oftentimes seem counterintuitive. The new role[latex]\,F\left(t\right)\,[/latex]uses the aforementioned outputs equally[latex]\,5\left(t\right),\,[/latex]merely matches those outputs to inputs 2 hours earlier than those of[latex]\,V\left(t\right).\,[/latex]Said another way, we must add ii hours to the input of[latex]\,V\,[/latex]to notice the corresponding output for[latex]F:F\left(t\correct)=V\left(t+2\correct).[/latex]

How To

Given a tabular role, create a new row to stand for a horizontal shift.

1. Identify the input row or column.
2. Decide the magnitude of the shift.
3. Add the shift to the value in each input jail cell.

Shifting a Tabular Function Horizontally

A function[latex]\,f\left(x\right)\,[/latex]is given in (Figure). Create a tabular array for the function[latex]\,g\left(ten\right)=f\left(x-three\right).[/latex]

[latex]10[/latex]	2	4	6	8
[latex]f\left(x\right)[/latex]	1	3	7	xi

Analysis

(Figure) represents both of the functions. Nosotros tin see the horizontal shift in each point.

Figure seven.

Identifying a Horizontal Shift of a Toolkit Function

(Figure) represents a transformation of the toolkit function[latex]\,f\left(ten\right)={x}^{2}.\,[/latex]Chronicle this new function[latex]\,yard\left(x\right)\,[/latex]to[latex]\,f\left(x\right),\,[/latex]and then find a formula for[latex]\,thousand\left(x\right).[/latex]

Figure 8.

Analysis

To determine whether the shift is[latex]\,+2\,[/latex]or[latex]\,-2[/latex], consider a unmarried reference bespeak on the graph. For a quadratic, looking at the vertex indicate is user-friendly. In the original function,[latex]\,f\left(0\right)=0.\,[/latex]In our shifted function,[latex]\,m\left(2\right)=0.\,[/latex]To obtain the output value of 0 from the function[latex]\,f,\,[/latex]nosotros need to decide whether a plus or a minus sign volition piece of work to satisfy[latex]\,g\left(two\right)=f\left(ten-2\right)=f\left(0\correct)=0.\,[/latex]For this to work, nosotros will demand to subtract two units from our input values.

Interpreting Horizontal versus Vertical Shifts

The office[latex]\,G\left(thou\right)\,[/latex]gives the number of gallons of gas required to drive[latex]\,m\,[/latex]miles. Interpret[latex]\,Thousand\left(m\correct)+10\,[/latex]and[latex]\,G\left(m+ten\right).[/latex]

Try It

Given the function[latex]\,f\left(ten\right)=\sqrt{ten},\,[/latex]graph the original function[latex]\,f\left(x\right)\,[/latex]and the transformation[latex]\,g\left(10\right)=f\left(10+2\right)\,[/latex]on the same axes. Is this a horizontal or a vertical shift? Which style is the graph shifted and past how many units?

Combining Vertical and Horizontal Shifts

Now that nosotros have two transformations, we can combine them. Vertical shifts are outside changes that affect the output (y-) values and shift the office up or down. Horizontal shifts are inside changes that affect the input (10-) values and shift the function left or correct. Combining the two types of shifts will crusade the graph of a function to shift upward or down and left or correct.

How To

Given a role and both a vertical and a horizontal shift, sketch the graph.

1. Identify the vertical and horizontal shifts from the formula.
2. The vertical shift results from a constant added to the output. Movement the graph up for a positive constant and down for a negative abiding.
3. The horizontal shift results from a constant added to the input. Move the graph left for a positive constant and right for a negative constant.
4. Utilize the shifts to the graph in either order.

Graphing Combined Vertical and Horizontal Shifts

Given[latex]\,f\left(x\correct)=|x|,\,[/latex]sketch a graph of[latex]\,h\left(ten\correct)=f\left(x+1\correct)-three.[/latex]

Try It

Given[latex]\,f\left(x\right)=|x|,\,[/latex]sketch a graph of[latex]\,h\left(ten\right)=f\left(x-2\right)+four.[/latex]

Show Solution

Identifying Combined Vertical and Horizontal Shifts

Write a formula for the graph shown in (Figure), which is a transformation of the toolkit foursquare root function.

Effigy 11.

Assay

Notation that this transformation has changed the domain and range of the part. This new graph has domain[latex]\,\left[1,\infty \right)\,[/latex]and range[latex]\,\left[ii,\infty \correct).[/latex]

Effort It

Write a formula for a transformation of the toolkit reciprocal part[latex]\,f\left(x\correct)=\frac{ane}{10}\,[/latex]that shifts the function'southward graph one unit of measurement to the right and i unit of measurement upwards.

Show Solution

[latex]g\left(x\right)=\frac{1}{10-one}+1[/latex]

Graphing Functions Using Reflections near the Axes

Another transformation that tin can be applied to a function is a reflection over the x– or y-axis. A vertical reflection reflects a graph vertically across the x-axis, while a horizontal reflection reflects a graph horizontally across the y-centrality. The reflections are shown in (Figure).

Figure 12. Vertical and horizontal reflections of a part.

Notice that the vertical reflection produces a new graph that is a mirror prototype of the base or original graph about the x-axis. The horizontal reflection produces a new graph that is a mirror paradigm of the base or original graph about the y-axis.

Reflections

Given a part[latex]\,f\left(x\correct),[/latex] a new function[latex]\,g\left(x\right)=-f\left(x\right)\,[/latex]is a vertical reflection of the role[latex]\,f\left(x\correct),\,[/latex]sometimes chosen a reflection about (or over, or through) the x-axis.

Given a function[latex]\,f\left(10\correct),\,[/latex]a new function[latex]\,thousand\left(x\correct)=f\left(-x\right)\,[/latex]is a horizontal reflection of the function[latex]\,f\left(10\right),\,[/latex]sometimes chosen a reflection about the y-axis.

How To

Given a function, reflect the graph both vertically and horizontally.

1. Multiply all outputs by –1 for a vertical reflection. The new graph is a reflection of the original graph about the x-axis.
2. Multiply all inputs past –1 for a horizontal reflection. The new graph is a reflection of the original graph most the y-centrality.

Reflecting a Graph Horizontally and Vertically

Reverberate the graph of[latex]\,south\left(t\right)=\sqrt{t}[/latex] (a) vertically and (b) horizontally.

Try It

Reverberate the graph of[latex]\,f\left(x\right)=|10-1|[/latex] (a) vertically and (b) horizontally.

Reflecting a Tabular Part Horizontally and Vertically

A part[latex]\,f\left(x\right)\,[/latex]is given equally (Figure). Create a tabular array for the functions below.

1. [latex]\,g\left(x\right)=-f\left(ten\right)[/latex]
2. [latex]\,h\left(x\correct)=f\left(-x\right)[/latex]

[latex]x[/latex]	two	four	6	8
[latex]f\left(ten\right)[/latex]	1	3	7	11

Endeavour It

A office[latex]\,f\left(x\right)\,[/latex]is given equally (Figure). Create a tabular array for the functions below.

1. [latex]g\left(10\correct)=-f\left(x\right)[/latex]
2. [latex]h\left(x\correct)=f\left(-ten\right)[/latex]

[latex]x[/latex]	−2	0	two	4
[latex]f\left(10\right)[/latex]	5	10	15	twenty

Applying a Learning Model Equation

A mutual model for learning has an equation similar to [latex]k\left(t\right)=-{2}^{-t}+one,\,[/latex] where [latex]k[/latex] is the percent of mastery that tin can exist achieved after [latex]t[/latex] exercise sessions. This is a transformation of the function [latex]f\left(t\correct)={2}^{t}[/latex] shown in (Effigy). Sketch a graph of [latex]k\left(t\correct).[/latex]

Figure 15.

Analysis

As a model for learning, this part would exist limited to a domain of[latex]\,t\ge 0,\,[/latex]with corresponding range[latex]\,\left[0,one\right).[/latex]

Attempt Information technology

Given the toolkit function[latex]\,f\left(x\right)={x}^{2},\,[/latex]graph[latex]\,g\left(x\right)=-f\left(x\right)\,[/latex]and[latex]\,h\left(x\correct)=f\left(-10\right).\,[/latex]Take notation of whatever surprising behavior for these functions.

Determining Even and Odd Functions

Some functions exhibit symmetry and then that reflections consequence in the original graph. For example, horizontally reflecting the toolkit functions [latex]f\left(ten\right)={x}^{2}[/latex] or [latex]f\left(10\right)=|ten|[/latex] volition result in the original graph. We say that these types of graphs are symmetric about the y-axis. A role whose graph is symmetric about the y-axis is called an fifty-fifty function.

If the graphs of[latex]\,f\left(ten\correct)={x}^{3}\,[/latex]or[latex]\,f\left(10\correct)=\frac{ane}{x}\,[/latex]were reflected over both axes, the result would be the original graph, as shown in (Effigy).

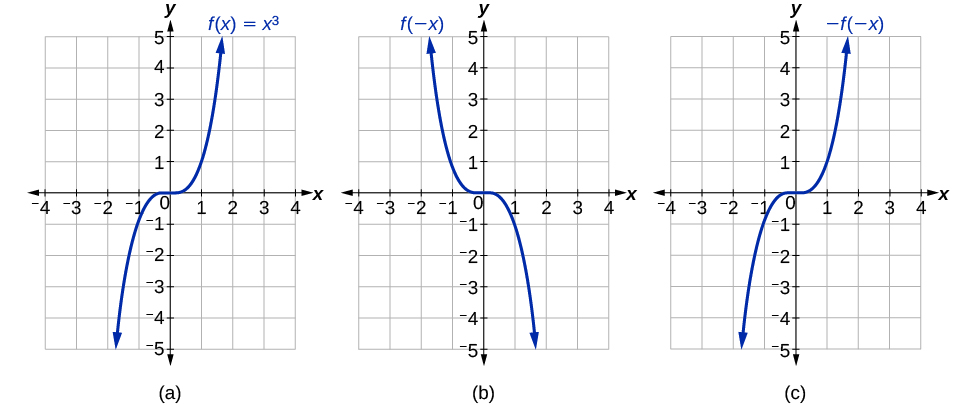
Figure 17. (a) The cubic toolkit role (b) Horizontal reflection of the cubic toolkit function (c) Horizontal and vertical reflections reproduce the original cubic function.

We say that these graphs are symmetric about the origin. A part with a graph that is symmetric about the origin is called an odd office.

Annotation: A function can exist neither fifty-fifty nor odd if it does not showroom either symmetry. For example,[latex]\,f\left(x\correct)={two}^{x}\,[/latex]is neither even nor odd. Likewise, the merely role that is both even and odd is the abiding office[latex]\,f\left(x\right)=0.[/latex]

Even and Odd Functions

A function is called an even function if for every input[latex]\,x[/latex]

[latex]f\left(x\right)=f\left(-ten\correct)[/latex]

The graph of an even role is symmetric about the [latex]y\text{-}[/latex]axis.

A role is chosen an odd role if for every input[latex]\,x[/latex]

[latex]f\left(10\right)=-f\left(-x\correct)[/latex]

The graph of an odd part is symmetric virtually the origin.

How To

Given the formula for a office, determine if the function is even, odd, or neither.

1. Determine whether the function satisfies[latex]\,f\left(10\correct)=f\left(-10\right).\,[/latex]If it does, it is even.
2. Make up one's mind whether the function satisfies[latex]\,f\left(x\right)=-f\left(-x\right).\,[/latex]If it does, it is odd.
3. If the function does not satisfy either rule, it is neither even nor odd.

Determining whether a Role Is Fifty-fifty, Odd, or Neither

Is the function[latex]\,f\left(x\right)={x}^{3}+2x\,[/latex]even, odd, or neither?

Analysis

Consider the graph of[latex]\,f\,[/latex]in (Figure). Notice that the graph is symmetric virtually the origin. For every point[latex]\,\left(x,y\right)\,[/latex]on the graph, the corresponding point[latex]\,\left(-10,-y\correct)\,[/latex]is likewise on the graph. For example, (one, 3) is on the graph of[latex]\,f,\,[/latex]and the corresponding point[latex]\left(-one,-3\correct)[/latex]is also on the graph.

Figure 18.

Effort It

Is the function[latex]\,f\left(s\right)={s}^{4}+3{south}^{ii}+7\,[/latex]fifty-fifty, odd, or neither?

Graphing Functions Using Stretches and Compressions

Adding a constant to the inputs or outputs of a office changed the position of a graph with respect to the axes, merely information technology did not bear on the shape of a graph. We now explore the effects of multiplying the inputs or outputs by some quantity.

We can transform the inside (input values) of a office or nosotros tin transform the outside (output values) of a function. Each change has a specific result that tin be seen graphically.

Vertical Stretches and Compressions

When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. If the constant is greater than 1, we get a vertical stretch; if the abiding is betwixt 0 and 1, we become a vertical pinch. (Effigy) shows a role multiplied by constant factors 2 and 0.5 and the resulting vertical stretch and pinch.

Figure 19. Vertical stretch and compression

Vertical Stretches and Compressions

Given a office[latex]\,f\left(x\correct),\,[/latex]a new function[latex]\,g\left(ten\right)=af\left(x\right),\,[/latex]where[latex]\,a\,[/latex]is a constant, is a vertical stretch or vertical pinch of the function[latex]\,f\left(ten\right).[/latex]

• If[latex]\,a>1,\,[/latex]then the graph volition exist stretched.
• If[latex]\,0<a<1,\,[/latex]and then the graph will be compressed.
• If[latex]\,a<0,\,[/latex]then there will be combination of a vertical stretch or compression with a vertical reflection.

How To

Given a function, graph its vertical stretch.

1. Identify the value of[latex]\,a.[/latex]
2. Multiply all range values by[latex]\,a.[/latex]

3. If[latex]\,\,a>ane,\,\,[/latex]the graph is stretched by a factor of[latex]\,a.[/latex]

   If[latex]\,0<a<1,\,[/latex]the graph is compressed by a factor of[latex]\,a.[/latex]

   If[latex]\,a<0,\,[/latex]the graph is either stretched or compressed and as well reflected about the 10-centrality.

Graphing a Vertical Stretch

A function[latex]\,P\left(t\correct)\,[/latex]models the population of fruit flies. The graph is shown in (Figure).

Effigy xx.

A scientist is comparison this population to another population,[latex]\,Q,\,[/latex]whose growth follows the aforementioned design, but is twice every bit large. Sketch a graph of this population.

How To

Given a tabular function and assuming that the transformation is a vertical stretch or compression, create a table for a vertical compression.

1. Determine the value of [latex]\,a.[/latex]
2. Multiply all of the output values by[latex]\,a.[/latex]

Finding a Vertical Pinch of a Tabular Function

A function[latex]\,f\,[/latex]is given as (Effigy). Create a table for the function[latex]\,yard\left(10\right)=\frac{1}{two}f\left(x\right).[/latex]

[latex]ten[/latex]	2	iv	6	viii
[latex]f\left(x\right)\,[/latex]	1	3	7	xi

Assay

The issue is that the function[latex]\,m\left(10\right)\,[/latex]has been compressed vertically past[latex]\,\frac{1}{2}.\,[/latex]Each output value is divided in one-half, then the graph is one-half the original height.

Try Information technology

A function[latex]\,f\,[/latex]is given equally (Effigy). Create a table for the role[latex]\,k\left(x\right)=\frac{3}{4}f\left(ten\right).[/latex]

[latex]x[/latex]	ii	4	six	8
[latex]f\left(ten\right)[/latex]	12	16	20	0

Recognizing a Vertical Stretch

The graph in (Figure) is a transformation of the toolkit office[latex]\,f\left(10\correct)={10}^{3}.\,[/latex]Relate this new part[latex]\,1000\left(x\right)\,[/latex]to[latex]\,f\left(x\right),\,[/latex]and then find a formula for[latex]\,thou\left(x\right).[/latex]

Figure 22.

Try It

Write the formula for the function that nosotros become when we stretch the identity toolkit part by a cistron of three, and so shift it downward past two units.

Show Solution

[latex]k\left(10\right)=3x-two[/latex]

Horizontal Stretches and Compressions

Now we consider changes to the inside of a role. When we multiply a part'southward input by a positive abiding, we become a part whose graph is stretched or compressed horizontally in relation to the graph of the original part. If the constant is betwixt 0 and 1, nosotros get a horizontal stretch; if the constant is greater than 1, nosotros get a horizontal compression of the function.

Effigy 23.

Given a function[latex]\,y=f\left(x\right),\,[/latex]the form[latex]\,y=f\left(bx\correct)\,[/latex]results in a horizontal stretch or compression. Consider the function[latex]\,y={10}^{2}.\,[/latex]Notice (Figure). The graph of[latex]\,y={\left(0.5x\right)}^{2}\,[/latex]is a horizontal stretch of the graph of the office[latex]\,y={x}^{2}\,[/latex]by a cistron of two. The graph of[latex]\,y={\left(2x\right)}^{2}\,[/latex]is a horizontal compression of the graph of the function[latex]\,y={x}^{2}\,[/latex]by a factor of 2.

Horizontal Stretches and Compressions

Given a function[latex]\,f\left(x\right),\,[/latex]a new part[latex]\,thou\left(10\correct)=f\left(bx\right),\,[/latex]where[latex]\,b\,[/latex]is a abiding, is a horizontal stretch or horizontal pinch of the office[latex]\,f\left(x\right).[/latex]

• If[latex]\,b>1,\,[/latex]then the graph volition be compressed by[latex]\,\frac{one}{b}.[/latex]
• If[latex]\,0<b<1,\,[/latex]then the graph volition be stretched by[latex]\,\frac{1}{b}.[/latex]
• If[latex]\,b<0,\,[/latex]then in that location volition be combination of a horizontal stretch or pinch with a horizontal reflection.

How To

Given a clarification of a function, sketch a horizontal compression or stretch.

1. Write a formula to represent the function.
2. Fix[latex]\,g\left(x\right)=f\left(bx\correct)\,[/latex]where[latex]\,b>one\,[/latex]for a compression or[latex]\,0<b<1\,[/latex]
   for a stretch.

Graphing a Horizontal Compression

Suppose a scientist is comparing a population of fruit flies to a population that progresses through its lifespan twice as fast every bit the original population. In other words, this new population,[latex]\,R,\,[/latex]will progress in i hour the same amount as the original population does in 2 hours, and in 2 hours, it will progress as much as the original population does in 4 hours. Sketch a graph of this population.

Analysis

Note that the effect on the graph is a horizontal pinch where all input values are half of their original distance from the vertical axis.

Finding a Horizontal Stretch for a Tabular Function

A office[latex]\,f\left(x\right)\,[/latex]is given equally (Figure). Create a table for the function[latex]\,g\left(x\right)=f\left(\frac{1}{2}x\right).[/latex]

[latex]x[/latex]	ii	iv	half dozen	viii
[latex]f\left(10\right)[/latex]	ane	3	seven	11

Assay

Considering each input value has been doubled, the issue is that the function[latex]\,g\left(x\right)\,[/latex]has been stretched horizontally past a factor of ii.

Recognizing a Horizontal Compression on a Graph

Relate the function[latex]\,grand\left(10\right)\,[/latex]to[latex]\,f\left(ten\right)\,[/latex]in (Figure).

Effigy 26.

Show Solution

The graph of[latex]\,g\left(x\right)\,[/latex]looks similar the graph of[latex]\,f\left(x\right)\,[/latex]horizontally compressed. Because[latex]\,f\left(x\right)\,[/latex]ends at[latex]\,\left(6,four\right)\,[/latex]and[latex]\,g\left(10\right)\,[/latex]ends at[latex]\,\left(ii,4\correct),\,[/latex]nosotros tin can run across that the [latex]\,10\text{-}[/latex]values have been compressed past[latex]\,\frac{one}{3},\,[/latex]because[latex]\,6\left(\frac{i}{three}\right)=two.\,[/latex]We might besides detect that[latex]\,g\left(2\right)=f\left(6\correct)\,[/latex]and[latex]\,g\left(1\right)=f\left(3\right).\,[/latex]Either way, we can describe this relationship equally[latex]\,g\left(10\right)=f\left(3x\right).\,[/latex]This is a horizontal compression past[latex]\,\frac{1}{3}.[/latex]

Analysis

Observe that the coefficient needed for a horizontal stretch or compression is the reciprocal of the stretch or compression. So to stretch the graph horizontally by a scale factor of 4, we demand a coefficient of[latex]\,\frac{1}{4}\,[/latex]in our part:[latex]\,f\left(\frac{1}{4}10\right).\,[/latex]This means that the input values must exist four times larger to produce the aforementioned issue, requiring the input to be larger, causing the horizontal stretching.

Attempt It

Write a formula for the toolkit square root function horizontally stretched by a factor of 3.

Show Solution

[latex]g\left(10\correct)=f\left(\frac{1}{3}x\correct)\,[/latex]then using the square root part we get[latex]\,yard\left(x\correct)=\sqrt{\frac{one}{three}x}[/latex]

Performing a Sequence of Transformations

When combining transformations, information technology is very important to consider the order of the transformations. For example, vertically shifting past 3 and then vertically stretching by 2 does not create the same graph as vertically stretching by 2 and so vertically shifting past three, because when we shift first, both the original function and the shift go stretched, while only the original office gets stretched when we stretch offset.

When we come across an expression such as[latex]\,\,2f\left(x\correct)+three,\,[/latex]which transformation should nosotros get-go with? The answer here follows nicely from the order of operations. Given the output value of[latex]\,f\left(x\correct),\,[/latex]we first multiply past 2, causing the vertical stretch, and then add 3, causing the vertical shift. In other words, multiplication before improver.

Horizontal transformations are a little trickier to think almost. When we write[latex]\,g\left(x\right)=f\left(2x+iii\right),\,[/latex]for example, nosotros have to call back about how the inputs to the function[latex]\,g\,[/latex]relate to the inputs to the part[latex]\,\,f.\,[/latex]Suppose we know[latex]\,f\left(7\right)=12.\,[/latex]What input to[latex]\,g\,[/latex]would produce that output? In other words, what value of[latex]\,x\,[/latex]will allow[latex]\,g\left(10\right)=f\left(2x+three\right)=12?\,[/latex]We would need[latex]\,2x+iii=7.\,[/latex]To solve for[latex]\,x,\,[/latex]nosotros would first subtract 3, resulting in a horizontal shift, and and then divide past 2, causing a horizontal compression.

This format ends up being very difficult to work with, because it is usually much easier to horizontally stretch a graph before shifting. We can work around this by factoring inside the part.

[latex]f\left(bx+p\right)=f\left(b\left(ten+\frac{p}{b}\right)\right)[/latex]

Let'south work through an instance.

[latex]f\left(x\right)={\left(2x+4\right)}^{2}[/latex]

We can cistron out a 2.

[latex]f\left(x\right)={\left(two\left(x+2\right)\right)}^{2}[/latex]

Now we can more clearly observe a horizontal shift to the left ii units and a horizontal pinch. Factoring in this way allows u.s.a. to horizontally stretch first and so shift horizontally.

Combining Transformations

When combining vertical transformations written in the form[latex]\,af\left(x\correct)+k,\,[/latex]first vertically stretch by[latex]\,a\,[/latex]and and so vertically shift by[latex]\,k.[/latex]

When combining horizontal transformations written in the form[latex]\,f\left(bx-h\right),\,[/latex]first horizontally shift by[latex]\,h\,[/latex]and so horizontally stretch past[latex]\,\frac{ane}{b}.[/latex]

When combining horizontal transformations written in the form[latex]\,f\left(b\left(ten-h\right)\right),\,[/latex]first horizontally stretch past[latex]\,\frac{1}{b}\,[/latex]and and then horizontally shift by[latex]\,h.[/latex]

Horizontal and vertical transformations are independent. Information technology does not matter whether horizontal or vertical transformations are performed beginning.

Finding a Triple Transformation of a Tabular Role

Given (Figure) for the role[latex]\,f\left(x\right),\,[/latex]create a tabular array of values for the function[latex]\,g\left(x\right)=2f\left(3x\right)+i.[/latex]

[latex]10[/latex]	half-dozen	12	eighteen	24
[latex]f\left(ten\right)[/latex]	10	14	15	17

Finding a Triple Transformation of a Graph

Utilize the graph of[latex]\,f\left(ten\right)\,[/latex]in (Effigy) to sketch a graph of[latex]\,k\left(x\correct)=f\left(\frac{1}{two}x+ane\right)-3.[/latex]

Figure 27.

Primal Equations

Vertical shift	[latex]g\left(ten\correct)=f\left(x\correct)+one thousand\,[/latex](upwardly for[latex]\,1000>0[/latex])
Horizontal shift	[latex]g\left(x\right)=f\left(x-h\right)[/latex](right for[latex]\,h>0[/latex])
Vertical reflection	[latex]g\left(ten\correct)=-f\left(ten\right)[/latex]
Horizontal reflection	[latex]thou\left(x\right)=f\left(-x\right)[/latex]
Vertical stretch	[latex]g\left(10\right)=af\left(ten\right)\,[/latex]([latex]a>0[/latex] )
Vertical compression	[latex]g\left(x\right)=af\left(10\right)\,[/latex][latex]\left(0<a<i\right)[/latex]
Horizontal stretch	[latex]g\left(x\right)=f\left(bx\right)[/latex][latex]\left(0<b<one\correct)[/latex]
Horizontal compression.	[latex]g\left(x\correct)=f\left(bx\right)\,[/latex]([latex]b>one[/latex])

Key Concepts

• A function can be shifted vertically by adding a abiding to the output. Come across (Figure) and (Figure).
• A function can be shifted horizontally past calculation a constant to the input. See (Figure), (Figure), and (Figure).
• Relating the shift to the context of a problem makes it possible to compare and interpret vertical and horizontal shifts. Encounter (Figure).
• Vertical and horizontal shifts are frequently combined. Meet (Figure) and (Figure).
• A vertical reflection reflects a graph most the [latex]\,ten\text{-}[/latex]axis. A graph tin be reflected vertically by multiplying the output past –1.
• A horizontal reflection reflects a graph well-nigh the [latex]y\text{-}[/latex]centrality. A graph tin can be reflected horizontally by multiplying the input past –1.
• A graph can be reflected both vertically and horizontally. The gild in which the reflections are applied does non affect the final graph. Come across (Effigy).
• A function presented in tabular form tin also be reflected past multiplying the values in the input and output rows or columns appropriately. Come across (Figure).
• A function presented as an equation can exist reflected by applying transformations one at a time. See (Figure).
• Fifty-fifty functions are symmetric nearly the [latex]y\text{-}[/latex]axis, whereas odd functions are symmetric about the origin.
• Even functions satisfy the condition[latex]\,f\left(ten\right)=f\left(-ten\right).[/latex]
• Odd functions satisfy the status[latex]\,f\left(x\correct)=-f\left(-ten\right).[/latex]
• A part tin be odd, even, or neither. See (Effigy).
• A function can be compressed or stretched vertically by multiplying the output by a abiding. Meet (Figure), (Figure), and (Figure).
• A function can be compressed or stretched horizontally past multiplying the input by a abiding. See (Effigy), (Figure), and (Figure).
• The lodge in which different transformations are applied does affect the terminal function. Both vertical and horizontal transformations must be practical in the order given. However, a vertical transformation may exist combined with a horizontal transformation in any order. Run across (Figure) and (Figure).

Section Exercises

Verbal

When examining the formula of a function that is the result of multiple transformations, how can y'all tell a horizontal shift from a vertical shift?

Show Solution

A horizontal shift results when a abiding is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.

When examining the formula of a function that is the result of multiple transformations, how tin you tell a horizontal stretch from a vertical stretch?

When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal pinch from a vertical compression?

Testify Solution

A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a abiding between 0 and 1 is multiplied by the output.

When examining the formula of a part that is the result of multiple transformations, how tin you tell a reflection with respect to the x-axis from a reflection with respect to the y-axis?

How can yous determine whether a function is odd or fifty-fifty from the formula of the function?

Show Solution

For a function[latex]\,f,\,[/latex]substitute[latex]\,\left(-x\right)\,[/latex]for[latex]\,\left(x\correct)\,[/latex]in[latex]\,f\left(10\right).\,[/latex]Simplify. If the resulting part is the same equally the original function,[latex]\,f\left(-x\right)=f\left(x\correct),\,[/latex]then the function is fifty-fifty. If the resulting function is the reverse of the original function,[latex]\,f\left(-x\right)=-f\left(x\correct),\,[/latex]then the original function is odd. If the office is not the same or the opposite, and then the function is neither odd nor fifty-fifty.

Algebraic

For the following exercises, write a formula for the function obtained when the graph is shifted as described.

[latex]\,f\left(x\right)=\sqrt{x}\,[/latex]is shifted up 1 unit of measurement and to the left 2 units.

[latex]\,f\left(ten\right)=|x|\,[/latex]
is shifted down 3 units and to the correct 1 unit.

Bear witness Solution

[latex]thousand\left(x\right)=|x-one|-3[/latex]

[latex]\,f\left(x\right)=\frac{one}{x}\,[/latex]is shifted down 4 units and to the correct 3 units.

[latex]\,f\left(ten\right)=\frac{i}{{x}^{ii}}\,[/latex]is shifted upwardly 2 units and to the left 4 units.

Show Solution

[latex]g\left(ten\right)=\frac{i}{{\left(x+iv\right)}^{2}}+2[/latex]

For the following exercises, draw how the graph of the function is a transformation of the graph of the original function[latex]\,f.[/latex]

[latex]y=f\left(x-49\right)[/latex]

[latex]y=f\left(10+43\correct)[/latex]

Show Solution

The graph of[latex]\,f\left(x+43\right)\,[/latex]is a horizontal shift to the left 43 units of the graph of[latex]\,f.[/latex]

[latex]y=f\left(x+3\right)[/latex]

[latex]y=f\left(x-4\right)[/latex]

Testify Solution

The graph of[latex]\,f\left(ten-4\right)\,[/latex]is a horizontal shift to the right 4 units of the graph of[latex]\,f.[/latex]

[latex]y=f\left(x\correct)+5[/latex]

[latex]y=f\left(x\right)+8[/latex]

Show Solution

The graph of[latex]\,f\left(ten\right)+8\,[/latex]is a vertical shift upwards 8 units of the graph of[latex]\,f.[/latex]

[latex]y=f\left(ten\right)-ii[/latex]

[latex]y=f\left(10\correct)-seven[/latex]

Show Solution

The graph of[latex]\,f\left(x\right)-vii\,[/latex]is a vertical shift downwardly 7 units of the graph of[latex]\,f.[/latex]

[latex]y=f\left(10-two\correct)+3[/latex]

[latex]y=f\left(x+4\right)-1[/latex]

Show Solution

The graph of [latex]f\left(x+iv\right)-i[/latex] is a horizontal shift to the left 4 units and a vertical shift downwardly 1 unit of the graph of [latex]f.[/latex]

For the post-obit exercises, determine the interval(s) on which the function is increasing and decreasing.

[latex]f\left(x\right)=4{\left(10+1\right)}^{2}-5[/latex]

[latex]1000\left(x\right)=5{\left(x+3\right)}^{two}-2[/latex]

Show Solution

decreasing on[latex]\,\left(-\infty ,-3\correct)\,[/latex]and increasing on[latex]\,\left(-iii,\infty \correct)[/latex]

[latex]a\left(x\correct)=\sqrt{-x+four}[/latex]

[latex]chiliad\left(x\right)=-3\sqrt{x}-1[/latex]

Show Solution

decreasing on [latex]\left(0,\,\infty \right)[/latex]

Graphical

For the following exercises, use the graph of[latex]\,f\left(x\right)={2}^{x}\,[/latex]shown in (Figure) to sketch a graph of each transformation of[latex]\,f\left(x\correct).[/latex]

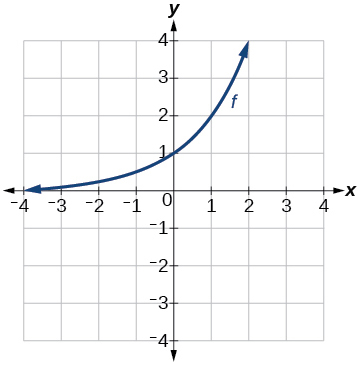
[latex]chiliad\left(x\correct)={two}^{x}+1[/latex]

[latex]h\left(x\right)={2}^{x}-3[/latex]

Show Solution

[latex]w\left(ten\right)={two}^{x-1}[/latex]

For the following exercises, sketch a graph of the function as a transformation of the graph of 1 of the toolkit functions.

[latex]f\left(t\right)={\left(t+i\right)}^{ii}-3[/latex]

Evidence Solution

[latex]h\left(x\right)=|ten-one|+4[/latex]

[latex]k\left(x\correct)={\left(x-two\right)}^{iii}-one[/latex]

Bear witness Solution

[latex]thou\left(t\right)=3+\sqrt{t+2}[/latex]

Numeric

Tabular representations for the functions[latex]\,f,\,thou,\,[/latex]and[latex]\,h\,[/latex]are given below. Write[latex]\,yard\left(x\right)\,[/latex]and[latex]\,h\left(x\right)\,[/latex]every bit transformations of[latex]\,f\left(x\right).[/latex]

[latex]ten[/latex]	−two	−1	0	1	2
[latex]f\left(x\right)[/latex]	−ii	−ane	−3	i	2

[latex]ten[/latex]	−1	0	1	two	3
[latex]g\left(x\right)[/latex]	−2	−one	−3	1	two

[latex]x[/latex]	−two	−i	0	ane	two
[latex]h\left(ten\right)[/latex]	−ane	0	−2	2	3

Show Solution

[latex]g\left(ten\correct)=f\left(x-1\correct),\,h\left(x\right)=f\left(x\right)+one[/latex]

Tabular representations for the functions[latex]\,f,\,k,\,[/latex]and[latex]\,h\,[/latex]are given beneath. Write[latex]\,g\left(10\correct)\,[/latex]and[latex]\,h\left(x\right)\,[/latex]as transformations of[latex]\,f\left(x\right).[/latex]

[latex]x[/latex]	−2	−1	0	ane	2
[latex]f\left(x\right)[/latex]	−one	−3	4	two	ane

[latex]ten[/latex]	−3	−2	−i	0	1
[latex]g\left(x\right)[/latex]	−1	−three	iv	2	1

[latex]x[/latex]	−two	−1	0	1	2
[latex]h\left(x\right)[/latex]	−2	−four	three	i	0

For the following exercises, write an equation for each graphed office by using transformations of the graphs of one of the toolkit functions.

Show Solution

[latex]f\left(x\right)=|x-iii|-two[/latex]

Testify Solution

[latex]f\left(x\right)=\sqrt{x+iii}-ane[/latex]

Bear witness Solution

[latex]f\left(10\correct)={\left(10-2\right)}^{2}[/latex]

Show Solution

[latex]f\left(10\right)=|x+3|-2[/latex]

For the following exercises, use the graphs of transformations of the square root function to find a formula for each of the functions.

Show Solution

[latex]f\left(ten\right)=-\sqrt{x}[/latex]

For the following exercises, use the graphs of the transformed toolkit functions to write a formula for each of the resulting functions.

Show Solution

[latex]f\left(x\right)=-{\left(x+1\right)}^{ii}+2[/latex]

Bear witness Solution

[latex]f\left(x\right)=\sqrt{-ten}+ane[/latex]

For the following exercises, determine whether the function is odd, even, or neither.

[latex]f\left(ten\right)=iii{ten}^{iv}[/latex]

[latex]grand\left(x\right)=\sqrt{x}[/latex]

[latex]h\left(x\right)=\frac{i}{x}+3x[/latex]

[latex]f\left(10\right)={\left(x-2\right)}^{2}[/latex]

[latex]thou\left(x\correct)=2{x}^{4}[/latex]

[latex]h\left(x\right)=2x-{ten}^{iii}[/latex]

For the following exercises, describe how the graph of each function is a transformation of the graph of the original office[latex]\,f.[/latex]

[latex]m\left(x\right)=-f\left(10\right)[/latex]

Bear witness Solution

The graph of[latex]\,g\,[/latex]is a vertical reflection (across the [latex]\,x[/latex]-axis) of the graph of[latex]\,f.[/latex]

[latex]thousand\left(x\right)=f\left(-x\right)[/latex]

[latex]g\left(x\correct)=4f\left(10\right)[/latex]

Bear witness Solution

The graph of[latex]\,chiliad\,[/latex]is a vertical stretch by a factor of iv of the graph of[latex]\,f.[/latex]

[latex]m\left(x\right)=6f\left(x\right)[/latex]

[latex]g\left(10\right)=f\left(5x\right)[/latex]

Show Solution

The graph of[latex]\,1000\,[/latex]is a horizontal compression by a factor of[latex]\,\frac{1}{5}\,[/latex]of the graph of[latex]\,f.[/latex]

[latex]thou\left(x\right)=f\left(2x\right)[/latex]

[latex]g\left(x\right)=f\left(\frac{1}{iii}ten\right)[/latex]

Show Solution

The graph of[latex]\,g\,[/latex]is a horizontal stretch past a factor of 3 of the graph of[latex]\,f.[/latex]

[latex]k\left(10\right)=f\left(\frac{1}{five}10\right)[/latex]

[latex]grand\left(x\right)=3f\left(-x\correct)[/latex]

Testify Solution

The graph of[latex]\,1000\,[/latex]is a horizontal reflection beyond the[latex]\,y[/latex]-axis and a vertical stretch by a factor of 3 of the graph of[latex]\,f.[/latex]

[latex]chiliad\left(x\right)=-f\left(3x\right)[/latex]

For the following exercises, write a formula for the function[latex]\,g\,[/latex]that results when the graph of a given toolkit function is transformed every bit described.

The graph of[latex]\,f\left(x\right)=|ten|\,[/latex]is reflected over the[latex]\,y[/latex]–axis and horizontally compressed by a cistron of[latex]\,\frac{1}{4}[/latex]
.

Show Solution

[latex]g\left(x\right)=|-4x|[/latex]

The graph of[latex]\,f\left(x\right)=\sqrt{x}\,[/latex]is reflected over the[latex]\,ten[/latex]-axis and horizontally stretched by a factor of two.

The graph of[latex]\,f\left(x\right)=\frac{one}{{x}^{ii}}\,[/latex]is vertically compressed by a factor of[latex]\,\frac{one}{three},\,[/latex]and then shifted to the left 2 units and down 3 units.

Bear witness Solution

[latex]one thousand\left(x\right)=\frac{1}{3{\left(ten+2\correct)}^{ii}}-three[/latex]

The graph of[latex]\,f\left(ten\right)=\frac{1}{10}\,[/latex]is vertically stretched past a factor of 8, and then shifted to the right 4 units and up 2 units.

The graph of[latex]\,f\left(10\right)={x}^{ii}\,[/latex]is vertically compressed by a gene of[latex]\,\frac{1}{two},\,[/latex]then shifted to the right five units and up 1 unit.

Show Solution

[latex]chiliad\left(x\right)=\frac{1}{2}{\left(ten-v\right)}^{2}+1[/latex]

The graph of[latex]\,f\left(x\right)={10}^{2}\,[/latex]is horizontally stretched past a factor of 3, then shifted to the left 4 units and down 3 units.

For the following exercises, draw how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.

[latex]g\left(x\right)=4{\left(x+1\right)}^{2}-5[/latex]

[latex]thou\left(x\correct)=v{\left(x+3\right)}^{two}-2[/latex]

[latex]h\left(x\right)=-2|x-4|+three[/latex]

[latex]thousand\left(x\right)=-3\sqrt{10}-i[/latex]

[latex]m\left(x\right)=\frac{ane}{ii}{x}^{3}[/latex]

[latex]north\left(x\correct)=\frac{1}{3}|ten-2|[/latex]

[latex]p\left(10\right)={\left(\frac{1}{3}x\right)}^{3}-3[/latex]

[latex]q\left(x\right)={\left(\frac{ane}{four}x\right)}^{iii}+ane[/latex]

[latex]a\left(10\right)=\sqrt{-x+4}[/latex]

For the following exercises, utilise the graph in (Figure) to sketch the given transformations.

[latex]g\left(x\correct)=f\left(x\right)-2[/latex]

[latex]g\left(10\right)=-f\left(ten\right)[/latex]

Show Solution

[latex]g\left(x\correct)=f\left(10+1\right)[/latex]

[latex]m\left(x\right)=f\left(x-2\right)[/latex]

Prove Solution

Glossary

even office

a function whose graph is unchanged by horizontal reflection,[latex]\,f\left(ten\right)=f\left(-10\correct),\,[/latex]and is symmetric nigh the [latex]y\text{-}[/latex]axis

horizontal compression

a transformation that compresses a function'due south graph horizontally, by multiplying the input by a constant[latex]\,b>ane[/latex]

horizontal reflection

a transformation that reflects a function'south graph across the y-axis by multiplying the input past[latex]\,-1[/latex]

horizontal shift

a transformation that shifts a part's graph left or right by calculation a positive or negative constant to the input

horizontal stretch

a transformation that stretches a function's graph horizontally past multiplying the input by a abiding[latex]\,0<b<1[/latex]

odd function

a function whose graph is unchanged by combined horizontal and vertical reflection,[latex]\,f\left(x\right)=-f\left(-10\right),\,[/latex]and is symmetric nigh the origin

vertical pinch

a function transformation that compresses the function'south graph vertically by multiplying the output by a constant[latex]\,0<a<1[/latex]

vertical reflection

a transformation that reflects a function's graph across the 10-axis by multiplying the output by[latex]\,-ane[/latex]

vertical shift

a transformation that shifts a function's graph up or downward by adding a positive or negative constant to the output

vertical stretch

a transformation that stretches a function's graph vertically by multiplying the output by a constant[latex]\,a>1[/latex]

pollackalownd.blogspot.com

Source: https://courses.lumenlearning.com/suny-osalgebratrig/chapter/transformation-of-functions/

Share this post